汽车电子机械制动系统的ABS自抗扰控制

baoshijie

引言

在汽车“新四化”的发展趋势下，制动系统迎来了革命性的变化。电子液压制动（electro-hydraulic brake,  EHB）系统和电子机械制动（electro-mechanical brake, EMB）系统2种形式的线控制动系统凭借结构简单、功能全面、性能可靠等优点受到国内外学者的广泛关注，同时越来越多的乘用车配备了以线控制动技术为基础的电子制动控制系统，例如防抱死制动系统（anti-lock braking system, ABS）、电子制动力分配系统（electrical brake distribution, EBD）等[1]。与EHB系统相比，EMB系统完全摒弃了液压装置，布局更简洁、响应更迅速，但它也存在非线性强、负载变化大、控制复杂等问题，在实际应用中仍面临诸多挑战[2] 。

ＡＢＳ作为一项提高车辆制动安全性的关键技术，能够保证车轮处于连续最佳制动状态，提高行车稳定性。目前车辆普遍装配的制动系统受到液压管路响应滞后的限制，并且大多数ABS仍采用基于大量道路实验的逻辑阈值控制方法，不利于提高车轮的附着性能[3]。基于EMB的ABS通过控制执行器的制动力主动调节车轮滑移率，使车轮持续获得峰值纵向附着力和较大的侧向附着力，缩短制动距离[4] 。

现有的研究大部分都是以液压、气压制动系统为基础，基于EMB的ABS控制策略研究较少。李顶根等[5]将EMB系统的控制器、电机和执行器视为一个闭环系统，通过控制基于滑移率的模糊控制器来调节夹紧力，使车轮滑移率保持在最佳值附近，采用了简化的EMB执行机构模型，降低了对EMB系统分析的完整性；杨坤等[6]使用EMB实现前、后轴之间的电子制动力分配，提出了一种基于模糊PID的ABS控制器，结果表明该控制器可以在不同种路面下准确控制各车轮的滑移率，但未能验证路面附着系数发生变化时的滑移率控制效果。Morselli等[7]提出了一种自校正ABS控制的 EMB系统，只通过测量车轮速度和估计车轮加速度来跟踪最佳滑移率值，但仿真结果超调较大，实际控制效果不佳。Li等[8]开发了一种采用自抗扰控制（active disturbance rejection control, ADRC）的ABS模型，并建立基于xPCTarget 的实时仿真平台，表明了ADRC在气压制动系统的ABS中能够对内外部扰动进行实时估计和补偿，使得车辆制动性能更加稳定，具有很强的鲁棒性。ADRC是韩京清教授继承了经典PID控制器的精髓，提出的一种几乎不依赖数学模型、实用性强的控制方法，ADRC解决了被控系统在平稳性与快速性之间的矛盾，该控制器已经在多个领域表现出优秀性能[9-11] 。

综上来看，基于EMB的 ABS控制既需要建立响应迅速、结构完备的执行器模型，也需要一种能够在非线性、不确定性系统中发挥良好控制作用的ABS控制器。基于此，提出了“行星齿轮减速机构 ＋滚珠丝杠 ＋活塞”的 ＥＭＢ执行器方案，以 ＡＤＲＣ理论为基础建立基于EMB的ABS控制器，实现对前、后车轮滑移率的准确控制。最后，通过ADRC模糊PID控制在不同路面工况下的对比仿真分析来验证所提策略的有效性。

１ 研究对象及工作原理

1.1 电子机械制动系统

EMB系统总体结构如图1所示，主要由电源、电子控制单元（electronic control unit, ECU）、电子制动踏板、通信线、制动执行器等主要部件构成[12] 。ECU是整个系统的核心，通过总线实现各模块的通讯。它在接收踏板模块的制动请求信号和各车轮轮速信号后，向车轮制动模块发送制动控制指令。EMB车轮制动模块由控制器和执行器组成，控制器发出控制信号作用于执行器，从而驱动电机产生相应制动力矩完成制动。



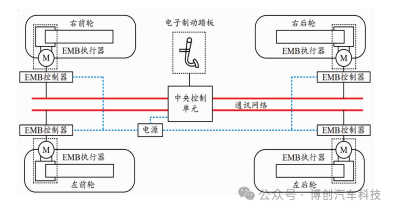
图1 EMB工作总体结构图

1.2  基于EMB的ABS工作原理

根据图2可知，车辆在行驶时，ECU收到驾驶员发出的紧急制动信号，并将信号传递到EMB电机控制器，驱动电机工作。减速装置将电机输出的力矩放大，运动转换装置将旋转运动转化为轴向运动，快速消除摩擦片与制动盘之间的制动间隙实现制动。此时，滑移率计算单元通过实时车速、轮速计算当前车轮滑移率，并和车辆行驶工况的最佳滑移率进行比较，反馈到ECU，最终将实时滑移率始终控制在目标滑移率的位置。



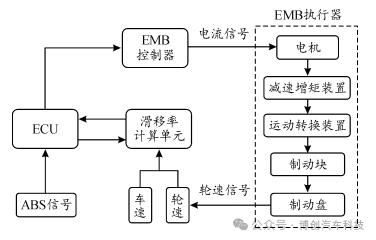
图2 基于 EMB的车辆单轮ABS工作原理图

EMB执行器采用“行星齿轮减速机构＋滚珠丝杠＋活塞”的设计方案，其三维结构如图3所示。



图3 EMB三维模型结构图

２ 车辆动力学系统建模

2.1 1/2车辆模型

如图4所示，考虑到在惯性的作用下，汽车在直道上制动时会发生前、后轴载荷转移的现象，建立了车辆1/2制动模型，假设前、后轴左、右车轮间所承受的载荷相等，并且忽略滚动阻力和空气阻力[13]。



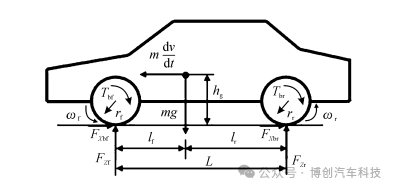
图4  1/2车辆制动模型示意图

图4中，ｍ为车辆的总质量；ｇ为重力加速度；rf和rr分别为前轮和后轮的半径；Tbf和Tbr分别为前轮和后轮制动器的制动力矩；ωｆ和 ωｒ分别为前轮和后轮的角速度；Ｌ为轴距；ｌｆ和 ｌｒ分别为前、后轴与质心之间的距离；ｈｇ为车辆质心高度；ｖ为车辆行驶的速度；FZf和 FZr分别为地面作用在前轮和后轮上的法向作用力；FXbf和FXbr分别为地面作用在前轮和后轮上的制动力。

车辆和轮胎的动力学方程可表示为：



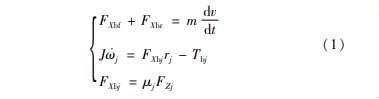
式中：ｊ为 ｆ、ｒ，分别表示前轮和后轮；Ｊ为车轮转动惯量；μｊ为前轮和后轮的纵向附着系数。

考虑到车辆在制动时前、后车轮载荷会发生转移，分别对前、后轮接地点取力矩可得前、后轮的地面制动力为：



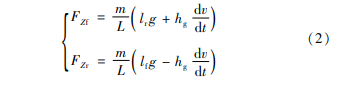
2.2 ＥＭＢ执行机构模型

2.2.1 电机模型

EMB电机选用无刷直流力矩电机，其动态方程[14]如下：



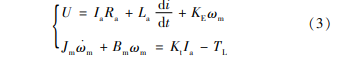
式中：U为电机电枢电压；当 Ia为电机电枢电流；Ra为电机电枢电阻；La为电机电枢电感；KE为电势系数；ωｍ 为电机转速；Jm为等效转动惯量；Bm为黏滞摩擦因数；TL 为负载转矩；Kt为电机转矩系数。

2.2.2 传动机构模型

传动机构包括所选用的行星齿轮减速机构和滚珠丝杠副，其作用是按照固定比例增大电机输出的力矩，并且将行星架的旋转运动转换成丝杠螺母的轴向位移。



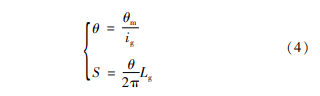
式中：θ为丝杠转角；θｍ 为电机转角；ig为减速装置传动比；S为丝杠螺母轴向位移；Lg为丝杠螺纹导程。

2.2.3 负载模型

当活塞推动制动块压紧制动盘后，电机堵转。此时，制动块上的摩擦片发生变形，其变形量与制动器的夹紧力存在非线性关系。

根据所采用的EMB执行机构方案进行试验并拟合数据，可得到变形量S与夹紧力Fb之间的关系[15]：



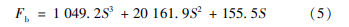
考虑到制动盘受到的夹紧力是由滚珠丝杠传递，因此EMB电机的负载转矩TL和制动器的输出力矩Tb可表示为：



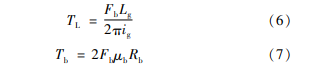
式中：μｂ为制动衬片摩擦因数；Rb为制动盘有效摩擦半径。

２．３ 轮胎模型

汽车在行驶过程中，随着制动力矩的增加，轮胎与地面会产生一定程度的相对滑动，车轮滑动部分在运动中所占的比例即为滑移率s，其计算公式可以表示为：



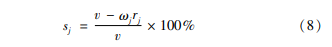
为了简化计算，采用Burckhardt等提出的半经验轮胎模型。纵向附着系数 μ与滑移率s的关系[16]可表示为：



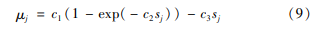
式中：c1、c2、c3为试验拟合得到的参数，可根据不同的路面附着系数取不同的值。

为了体现典型工况的特征，选择用如图5所示的高附着路面、中附着路面及低附着路面来描述3种不同附着系数等级的工况，其各自的最佳滑移率sref可通过计算得到[17] 。



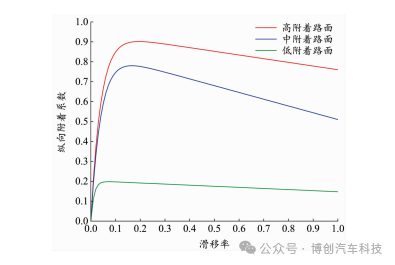
图5 滑移率 －纵向附着系数关系曲线

３ 基于ADRC的 ABS控制

ADRC继承了PID控制的优点，它利用观测器来估计扰动，并且通过非线性方式来组合状态反馈，因此在控制具有不确定性和时变性的非线性模型方面具有明显优势。ADRC由跟踪 －微分器(TD)、扩展状态观测器(ESO)和非线性状态误差反馈控制率(NLSEF３个模块组成，其结构如图6所示[18]。图中，u1为输入信号sref 的跟踪信号；u2为u1的微分信号；z1、z2、z3为系统状态变量估计误差；i0为非线性状态误差反馈控制量，i为输入到被控系统的控制量；ｂ为增益系数；b0为增益系数的估计值。



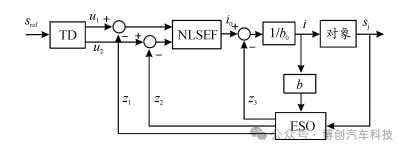
图6  二阶ADRC控制结构图

3.1  滑移率控制模型

对式(9)关于时间求导，并将式(1)代入整理可得：



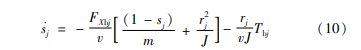
考虑到车辆在制动时，制动执行器夹紧制动盘，ＥＭＢ电机发生堵转，电机输出的力矩Tb与给定的电机电枢电流 Ia近似成正比关系。因此，将式（１０）改写为非线性二阶自抗扰控制器的状态方程：



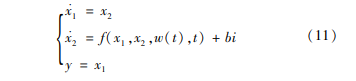
令：



式中，f(x1. x2, w(t) )为系统内、外部扰动总和。

3.2  扩张状态观测器设计

ESO是整个ADRC的核心，它将系统的总扰动扩张成一个新的状态变量，根据系统的输入与输出估计出系统的原有状态。建立ESO的观测方程：



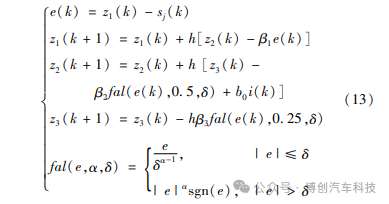
式中：h为采样步长；δ为线性段区间长度。

3.3 跟踪 －微分器设计

TD的作用是安排系统的过渡过程，并且对信号进行滤波，得到微分信号，具体设计过程如下。

利用最速综合函数 fhan(u1, u2, r, h0):



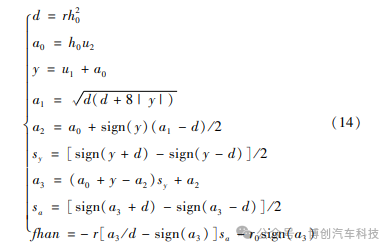
建立目标滑移率跟踪方程：



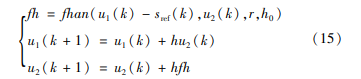
式中：r为控制量增益；h0为滤波因子，其值通常取采样步长hｈ的整数倍。

3.4 非线性状态误差反馈控制率设计

NLSEF将TD和ESO输出量之间的误差进行非线性组合，从而获得误差反馈控制量。



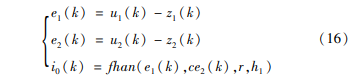
式中：ｃ为阻尼因子；h1为精度因子。

综上，可得控制量：



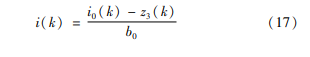
4 仿真分析

4.1 EMB响应性能分析

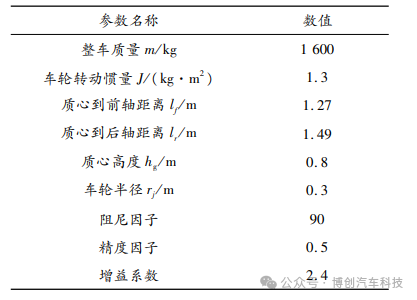
为了验证所采用EMB执行器方案的响应性能，首先在 Matlab/Simulink中进行仿真验证，其主要参数如表1所示。

表1 EMB执行器主要参数



在仿真时，输入一个从 ２４ｋＮ→４ｋＮ→１４ｋＮ→１６ｋＮ阶跃变化的目标夹紧力信号（每个信号持续 １ｓ）来模拟驾驶员在紧急制动和连踩制动踏板制动工况下 ＥＭＢ执行器的性能，图 ７、图 ８为 ＥＭＢ的电流、夹紧力响应曲线。

由图７、图８可知，当EMB执行器收到制动命令后，电机快速启动，电流经过启动突变后从0.04s开始增大，在0.31s达到电机堵转的稳态值。而夹紧力在消除制动间隙后也迅速上升，经过0.24s达到目标制动夹紧力24kN，比文献[19]中要求的24kN制动夹紧力目标响应时间(0.3s)快了20％。



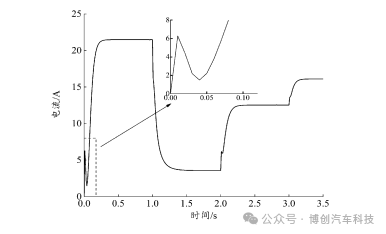
图7 EMB电流响应曲线



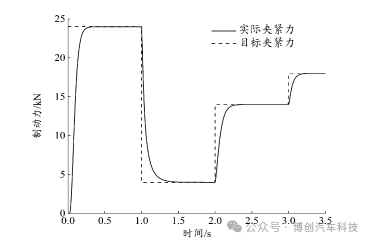
图8 EMB夹紧力响应曲线

当仿真开始1s后，目标夹紧力下降至4kN并每隔1s发生阶跃，此时夹紧力仍然具有良好的响应能力，特别是在跟踪响应初始阶段，可以稳定、快速、准确地达到所需的目标夹紧力。

4.2基于EMB的ABS控制器仿真分析

如图9所示，建立基于ADRC的ABS双轮制动模型。在仿真中，共取单一路面、对接路面 ２种制动试验工况，为突出基于滑移率的ADRC的优势，与文献[20]中所采用的模糊PID控制进行对比。其中车辆制动的初始速度设置为20ｍ/s，当车辆速度降到2.78m/s退出ABS控制，其他仿真主要参数如表2所示。



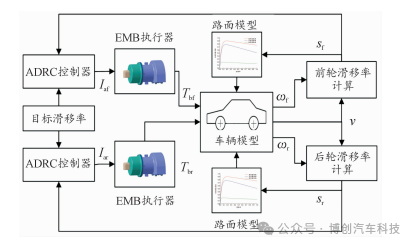
图9 基于ADRC的 ABS双轮制动模型结构示意图

表2 ABS仿真主要参数



4.2.1 单一路面工况仿真

本次仿真以目标滑移率为0.06的低附着路面为例进行分析，不同控制方案的制动过程结果如图10—图12所示。在附着系数较低的路面上进行紧急制动时, EMB执行器能快速做出响应，并且由于车辆在制动时会出现前、后轴载荷转移的现象，因此制动初始阶段前轮的载荷增加，导致其制动力大于后轮制动力，前轮车速下降得更快，前轮滑移率也要先于后轮达到目标滑移率。由图10、图 11可知，采用ADRC的车辆能够更快地将车速与轮速降到0，并且与模糊PID控制相比，其总制动时间减少了0.43s，总制动距离缩短了6.7m。



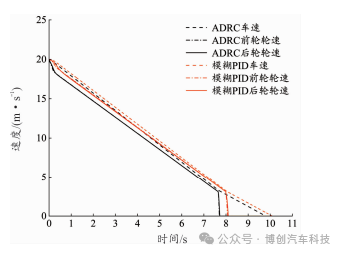
图10 低附着路面速度曲线



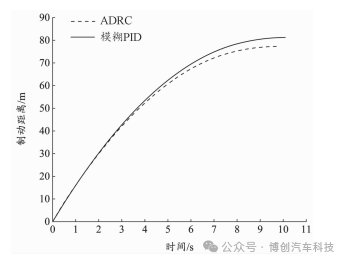
图11 低附着路面制动距离曲线



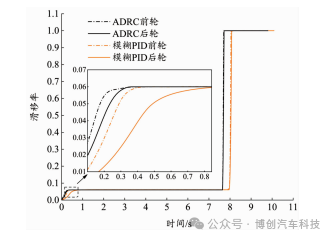
图12 低附着路面滑移率曲线

在滑移率跟踪方面，２种控制方案皆能够有效保持滑移率的稳定，直到车速低于 ２．１８ｍ／ｓ时，车辆退出 ＡＢＳ，前、后轮滑移率突变为 １。由图 １２可知，滑移率曲线并未出现明显超调现象，但是基于滑移率的 ＡＤＲＣ前、后轮到达目标滑移率的时间分别要比模糊 ＰＩＤ控制快 ０．１１ｓ和 ０．５３ｓ。可知基于 ＡＤＲＣ的 ＡＢＳ响应速度更快，充分保证了车辆制动的安全性。

4.2.2 对接路面工况仿真

在本次仿真中，以中附着 －高附着对接路面为例进行分析，假设路面在开始制动后的 １５ｍ处从中附着变为高附着路面，此时目标滑移率从 ０．１３变为 ０．１７，不同控制方案的制动过程结果如图 １３—图 １５所示。



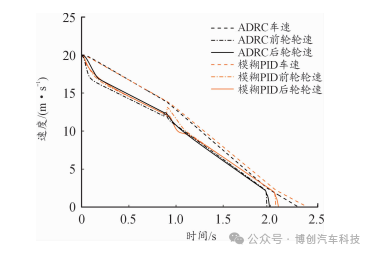
图13 中附着 －高附着对接路面速度曲线



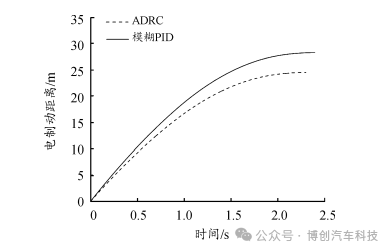
图14 中附着 －高附着对接路面制动距离曲线



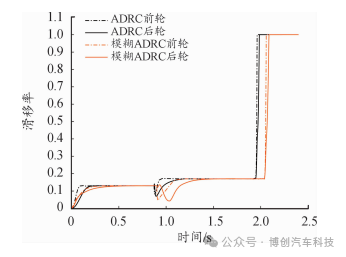
图15 中附着 －高附着对接路面滑移率曲线

由图13、图14可知，制动开始时2种控制方案的车速与轮速都快速下降，在路面附着系数突变时，ADRC的波动幅度明显小于模糊PID控制，前者的制动时间与制动距离分别比后者减少了5.1%和14.5％。

在滑移率跟踪方面，由图15可知, 2种控制下的前、后轮滑移率都能够稳定在目标滑移率处，但是当路面附着系数发生变化时，采用模糊PID控制的轮速出现明显的响应时滞，其前、后轮达到目标滑移率0.17的时间分别要比采用ADRC的滞后0.15s和 0.31ｓ。因此ADRC在面对扰动时，具备控制精度高、稳定性强、抗干扰的优点，有利于更好地实现车辆的ABS功能。

５ 结论

针对具有不确定性的电子机械制动系统ABS控制问题，提出了“行星齿轮减速机构＋滚珠丝杠 ＋活塞”的EMB执行器方案，并基于滑移率开发了一种ABS自抗扰控制策略，提高系统的抗干扰性。研究结果表明：

１）所提出的EMB执行器完成制动间隙消除后，在0.24s达到24kN的目标夹紧力，比目标响应时间降低了20%，有效解决了制动响应滞后的问题。

２）与模糊PID控制相比，在不同路面工况下，ADRC能够更快将车轮滑移率稳定在目标值，缩短了制动距离与制动时间，提高车辆在紧急制动时的安全性。

在下一阶段，将对现有控制器进行改进，使ADRC的参数能够自适应调节；研究汽车在转弯制动工况的ABS控制，并且加入实车试验。

参考文献：

[1]张玉新，何文钦，陈虹，等．自动驾驶汽车安全技术专利分析综述[J]．中国科学：信息科学，2020, 50(11):1732-1755．

[2]XIAOF, GOMGXX, LUZH, etal. Design and control of new brake-by-wire actuator for vehicle based on liner motor and lever mechanism [J]. IEEE Access, 2021, 9: 95832-95842.

[3] 郝亮，郭立新，张旭斌，等．汽车 ＡＢＳ控制算法设计与试验验证[J]．机械设计与制造, 2019(11): 221-223.

[4] 常九健，张煜帆．基于 ＥＭＢ的纯电动汽车制动能量回收优化控制策略研究[J]．汽车工程, 2022, 44(1):64-72.

[5] 李顶根，张绿原，何保华．基于滑移率的汽车电子机械制动系统的模糊控制[J]．机械工程学报，2012, 48(20): 124-129.

[6] 杨坤，李静，李幼德，等．基于汽车电子机械制动系统的EBD/ABS研究[J]．系统仿真学报, 2009, 21(6): 1785-1788.

[7]MORSELLIR, AZNASIR. A self-tuning ABS control for electro mechanical braking systems [J]. IFAC Proceedings Volumes, 2006, 39(16): 620-625.

[8]LIWJ, ZHANGQ, ZHANGY. The effect of ADRC on vehicle braking performance [J]. Journal of Electrical Engineering & Technology, 2020, 15(2): 705-712.

[9] 韩京清．从PID技术到“自抗扰控制”技术[J]．控制工程，2022, 9(3): 13-18.

[10] 李冰林，曾励，张鹏铭，等．主动磁悬浮轴承的滑模自抗扰解耦控制[J]．电机与控制学报, 2021, 256(7): 129-138.

[11] 刘艺，刘宝泉，鲁毛毛，等．混合式步进电机自抗扰控制器状态观测反馈优化方法[J]．重庆理工大学学报（自然科学）, 2022, 36(10): 208-215.

[12] 程洁，郑凯，秦嘉，等．面向智能车辆的 ＥＭＢ系统功能安全分析及应用设计[J]．汽车安全与节能学报, 2023, 14(1): 69-79.

[13] 彭晓燕，何磊，吕以滨．基于滑移率的电子机械制动模糊滑模控制[J]．中南大学学报（自然科学版）, 2018, 49(2): 360-370.

[14] 刘志强，王振，陈玉锦．电子机械制动器的建模、仿真和实验研究[J]．机电工程, 2023, 40(4): 485-493.

[15] 刘志强，陈玉锦，陈林．电子机械制动器的间隙调控方法[J]．兵工学报, 2022, 43(7): 1478-1487．

[16] 段敏，郭文涛，李刚，等．两轮独立驱动电动汽车驱动防滑控制研究[J]．辽宁工业大学学报（自然科学版）, 2016, 36(4):257-261.

[17] APAROW VR, AHMADF, HUDHAK, etal. Modelling and PID control of antilock braking system with wheels slip reduction to improvr braking performance[J]. International journal of Vehicles Safety, 2013, 6(3): 265-296.

[18] ZHANG, YANGZ, ZHOUGX, etal. Adaptive fuzzy actived disturbance rejection control based reconfiguration conturoller design for aircraft anti-skid braking system[J]. Actuators, 2021, 10(8): 201.

[19] 夏利红，邓兆祥．电子机械制动执行器的整体最优匹配设计[J]．吉林大学学报（工学版）, 2018, 48(4): 998-1007．

[20] XIELJ, YANGW H. Simulation study on automotive EMB system based on self-tuning fuzzy PID control [J]. Acta Technica CSAV (Ceskoslovensk Akademie Ved), 2017, 62(1):103-116.

lixinfu

针对汽车电子机械制动系统的ABS自抗扰控制，我作为汽车工程师给出以下回复：

随着汽车“新四化”的推进，电子机械制动系统已成为研究的热点。其中，ABS自抗扰控制在EMB系统中发挥着重要作用。该技术通过精确控制制动压力，有效避免车轮抱死，提高车辆的制动性能和行驶稳定性。其结构简单、功能全面、性能可靠，正受到越来越多学者的关注。同时，越来越多的乘用车已配备基于线控制动技术的电子制动控制系统，其中ABS和EBD系统是关键组成部分。对于未来的汽车制动系统，我预期其将更加智能化、高效化，为驾驶者提供更加安全、舒适的驾驶体验。